Conducting mixed effect/trajectory analysis using DataSHIELD
Source:vignettes/ds-helper-trajectories-vignette.Rmd
ds-helper-trajectories-vignette.RmdIntroduction
Overview
This tutorial will demonstrate how to model trajectories in DataSHIELD using repeated measures data from multiple cohorts.
This tutorial draws on the following papers/tutorials:
Hughes, R., Tilling, K. & Lawlor, D. Combining longitudinal data from different cohorts to examine the life-course trajectory. Preprint available on medrxiv: https://doi.org/10.1101/2020.11.24.20237669
Tilling K, Macdonald-Wallis C, Lawlor DA, Hughes RA, Howe LD. Modelling childhood growth using fractional polynomials and linear splines. Ann Nutr Metab. 2014;65(2-3):129-38. https://doi.org/10.1159/000362695.
Centre for Multilevel Modelling online course. http://www.bristol.ac.uk/cmm/learning/online-course/
You will use simulated data to replicate part of the analysis from Hughes et al. cited above. It would be helpful to read this tutorial in conjuncture with this paper.
Please note that not all the methods used in Hughes et al. are available in DataSHIELD. Currently it is not possible to do 1-stage meta-analysis of mixed effects models. All of these are in the pipeline and this tutorial will be extended when these methods become available.
Do spline models!
Installing and loading packages
First you need to install some packages are used in tutorial. Even if you have previously installed them it is worth doing this again to ensure that you have the latest versions.
If prompted to update packages, select option ‘none’.
First install the package ‘remotes’ which contains the function ‘install_github’.
#install_github("datashield/DSI")
#install_github("datashield/dsBaseClient")
#install_github("lifecycle-project/ds-helper", ref = "dev")
#install.packages("DSMolgenisArmadillo")
#install.packages("tidyverse")Now we load these packages.
library(dsBaseClient)
library(DSI)
library(DSMolgenisArmadillo)
library(dsHelper)
library(tidyverse)A couple of things to note:
I use a lot of the tidyverse packages as I find them very efficient and they make the code more readable. If any syntax is unclear just ask!
I also use a number of functions from a package called dsHelper. This was written by me and Sido Haakma to make analysis in DataSHIELD more straightforward. Any problems with these functions just let us know.
Logging in and assigning data
The simulated data is held on a remote server. To access it, you first request a ‘token’ which contains the login details. You then use this to login and assign the data.
url <- "https://armadillo-demo.molgenis.net/"
token <- armadillo.get_token(url)
builder <- DSI::newDSLoginBuilder()
builder$append(
server = "alspac",
url = url,
table = "trajectories/data/alspac",
token = token,
driver = "ArmadilloDriver",
profile = "xenon")
builder$append(
server = "bcg",
url = url,
table = "trajectories/data/bcg",
token = token,
driver = "ArmadilloDriver",
profile = "xenon")
builder$append(
server = "bib",
url = url,
table = "trajectories/data/bib",
token = token,
driver = "ArmadilloDriver",
profile = "xenon")
builder$append(
server = "probit",
url = url,
table = "trajectories/data/probit",
token = token,
driver = "ArmadilloDriver",
profile = "xenon")
logindata <- builder$build()
conns <- DSI::datashield.login(logins = logindata, assign = T, symbol = "data")We can check that this has worked. You should see that each cohort has one dataframe called “data”, which contains 7 variables.
ds.summary("data")## $alspac
## $alspac$class
## [1] "data.frame"
##
## $alspac$`number of rows`
## [1] 129681
##
## $alspac$`number of columns`
## [1] 7
##
## $alspac$`variables held`
## [1] "id" "age" "sex" "ethnicity" "father_socialclass" "mother_education"
## [7] "weight"
##
##
## $bcg
## $bcg$class
## [1] "data.frame"
##
## $bcg$`number of rows`
## [1] 12724
##
## $bcg$`number of columns`
## [1] 7
##
## $bcg$`variables held`
## [1] "id" "age" "sex" "ethnicity" "father_socialclass" "mother_education"
## [7] "weight"
##
##
## $bib
## $bib$class
## [1] "data.frame"
##
## $bib$`number of rows`
## [1] 68864
##
## $bib$`number of columns`
## [1] 7
##
## $bib$`variables held`
## [1] "id" "age" "sex" "ethnicity" "father_socialclass" "mother_education"
## [7] "weight"
##
##
## $probit
## $probit$class
## [1] "data.frame"
##
## $probit$`number of rows`
## [1] 191224
##
## $probit$`number of columns`
## [1] 7
##
## $probit$`variables held`
## [1] "id" "age" "sex" "ethnicity" "father_socialclass" "mother_education"
## [7] "weight"We wont be using all of the variables today, however if you want to come back and use this data to try out more complicated models we’ll keep it online.
Part 1: Visualising the data
Scatter plots of child weight by age
Let’s start off by looking at our repeated measures weight data for each cohort. We can make scatter plots with age on the x-axis and weight on the y-axis.
Note that the values that you see are anonymised - they are a non-disclosive approximation of the original values.
ds.scatterPlot(x = "data$age", y = "data$weight")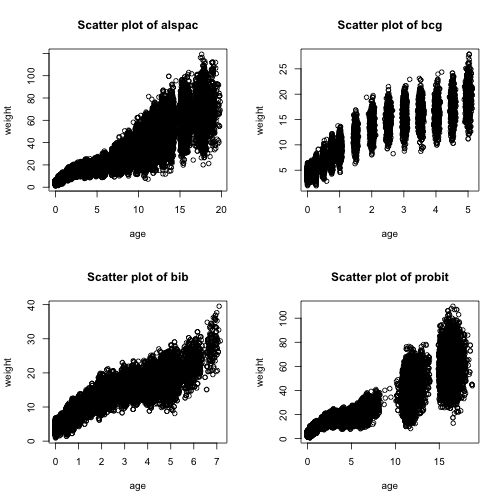
## [1] "Split plot created"What are you initial thoughts about the data?
Mean observed weight by age
Another way to visualise the weight data is to split child age into yearly intervals, and plot the mean on the y-axis with age on the x-axis (see Figure 2 from Hughes et al.).
First of all we need to calculate the mean values for weight at each yearly age band:
mean_age <- dh.meanByGroup(
df = "data",
outcome = "weight",
group_var = "age")## # A tibble: 55 × 3
## cohort age mean
## <chr> <dbl> <dbl>
## 1 alspac 0 4.64
## 2 alspac 1 8.78
## 3 alspac 2 12.8
## 4 alspac 3 16.1
## 5 alspac 4 17.0
## 6 alspac 5 18.4
## 7 alspac 6 20.3
## 8 alspac 7 24.3
## 9 alspac 8 26.5
## 10 alspac 9 30.5
## 11 alspac 10 35.1
## 12 alspac 11 38.8
## 13 alspac 12 43.6
## 14 alspac 13 49.3
## 15 alspac 14 54.6
## 16 alspac 15 61.3
## 17 alspac 16 63.5
## 18 alspac 17 67.0
## 19 alspac 18 67.7
## 20 alspac 19 70.8
## 21 alspac 20 71.8
## 22 bcg 0 5.11
## 23 bcg 1 8.88
## 24 bcg 2 13.3
## 25 bcg 3 15.4
## 26 bcg 4 16.4
## 27 bcg 5 18.6
## 28 bib 0 4.46
## 29 bib 1 8.11
## 30 bib 2 13.3
## 31 bib 3 16.0
## 32 bib 4 17.1
## 33 bib 5 18.7
## 34 bib 6 22.4
## 35 bib 7 27.8
## 36 probit 0 4.98
## 37 probit 1 8.66
## 38 probit 2 14.0
## 39 probit 3 16.4
## 40 probit 4 16.8
## 41 probit 5 17.8
## 42 probit 6 20.8
## 43 probit 7 23.6
## 44 probit 8 28.0
## 45 probit 9 34.6
## 46 probit 10 36.1
## 47 probit 11 39.8
## 48 probit 12 42.1
## 49 probit 13 47.1
## 50 probit 14 54.0
## 51 probit 15 60.1
## 52 probit 16 62.4
## 53 probit 17 63.2
## 54 probit 18 61.6
## 55 probit 19 61.0Now we have the values locally, we can use any r package to plot these. I like to use ggplot:
palette <- c("#264653", "#2a9d8f", "#E9C46A", "#F4A261", "#E76F51")
mean_age.plot <- ggplot() +
geom_line(data = mean_age, aes(x = age, y = mean, colour = cohort), linewidth = 0.8) +
scale_y_continuous(limit = c(0, 80), breaks = seq(0, 80, 20), expand = c(0, 0)) +
xlab("Child age") +
ylab("Observed weight (KG)") +
scale_colour_manual(values = palette)
mean_age.plot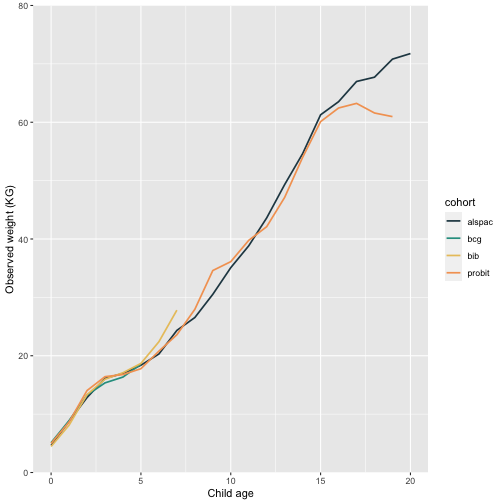
Q: Looking at these two plots, What are your initial thoughts about the pattern of weight change over time?
Describing the exposures
DataSHIELD contains the functions ds.summary and ds.table which can be used to describe continuous and categorical variables. However, the output of these is a little tricky to work with. Instead we can use the function ‘dh.getStats’ to extract descriptives in a more usable format.
stats <- dh.getStats(
df = "data",
vars = "sex")
stats## $categorical
## # A tibble: 0 × 10
## # ℹ 10 variables: variable <chr>, cohort <chr>, category <chr>, value <dbl>, cohort_n <int>, valid_n <dbl>, missing_n <dbl>, perc_valid <dbl>,
## # perc_missing <dbl>, perc_total <dbl>
##
## $continuous
## # A tibble: 5 × 15
## variable cohort mean std.dev perc_5 perc_10 perc_25 perc_50 perc_75 perc_90 perc_95 valid_n cohort_n missing_n missing_perc
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 sex alspac 0.49 0.5 0 0 0 0 1 1 1 129681 129681 0 0
## 2 sex bcg 0.48 0.5 0 0 0 0 1 1 1 12724 12724 0 0
## 3 sex bib 0.49 0.5 0 0 0 0 1 1 1 68864 68864 0 0
## 4 sex probit 0.48 0.5 0 0 0 0 1 1 1 191224 191224 0 0
## 5 sex combined 0.49 0.5 0 0 0 0 1 1 1 402493 402493 0 0This gives us a list with two elements corresponding to the continuous and categorical variables. As we didn’t request stats for any continuous variables, the first list is empty.
Some more descriptives that are useful to have
There are other bits of information it is useful to report:
- Total number of observations
- Total number of participants
- Min and max age of participants
- Median number of measurements per individual
We can use the function dh.getRmStats to extract this info. Note that the min and max ages are based on the 5th and 95th percentiles as DataSHIELD doesn’t will not return true minimum and maximums due to disclosure issues.
rm_stats <- dh.getRmStats(
df = "data",
outcome = "weight",
id_var = "id",
age_var = "age")
rm_stats## # A tibble: 5 × 8
## cohort min_age max_age n_obs n_participants n_meas_5 n_meas_med n_meas_95
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 alspac 0 15.7 129681 14216 6 9 13
## 2 bcg 0 4.99 12724 951 12 14 14
## 3 bib 0 4.98 68864 13445 3 5 8
## 4 probit 0 15.9 191224 17046 9 11 14
## 5 combined 0 13.6 402493 45658 6.36 8.67 11.9Part 2: Fitting a simple linear trajectory
Trajectory models: prep
Before we can get started, we need to make sure that our id variable is an integer. If we don’t, it breaks. First we create a new object which is an integer version of our ID. We then join this back to our main dataframe.
ds.asInteger(
x.name = "data$id",
newobj = "id_int")
ds.dataFrame(
x = c("data$id", "data$age", "data$sex", "data$ethnicity",
"data$father_socialclass", "data$mother_education", "data$weight",
"id_int"),
stringsAsFactors = F,
newobj = "data")Specifying the model
First we fit a model with weight predicted by four terms: an intercept (1), age, sex and the interaction between age and sex. These terms are our ‘fixed effects’, and comprise the first half of the formula below. They are specified in the same way as you would write a formula in a standard regression model.
In the second half of the formula below we specify our random effects. This is where we provide information about how we believe the data to be clustered.
The variable to the right of the vertical line is our ID variable. This specifies that we want to treat each invidual as a separate cluster, because we believe their measurements will be correlated. This is a plausible hypothesis: for example if my height is a lot higher than average at age 5, it is likely to also be higher than average at age 10. We can describe this as a 2-level clustering, with weight measurements (level 1) clustered within individuals (level 2).
The variables to the left of the vertical line specify which extra parameters we want to estimate for each individual. Or to put it another way, it specifies which parameters we allow to vary for each individual.
If we just specify “1”, then in addition to calculating an overall intercept, we also calculate an intercept for each individual. This provides us with information about the variability between individuals in their starting weight. This is called a random intercept model.
If we specifed “1 + age”, then in addition we would calculate a separate slope for each individual. This would provide us with information about how the gradient of the trajectory varies between individuals. This is called a random slope model.
Here we start with a random intercept model. Understand what you are doing is the difficult bit; fitting the model is straightfoward:
model1.fit <- ds.lmerSLMA(
dataName = "data",
formula = "weight ~ 1 + age + sex + age*sex + (1|id_int)",
datasources = conns)
model1.fit$output.summary## $study1
## Linear mixed model fit by REML ['lmerMod']
## Formula: weight ~ 1 + age + sex + age * sex + (1 | id_int)
## Data: dataDF
## Weights: weights.to.use
## Offset: offset.to.use
## Control: control.obj
##
## REML criterion at convergence: 839458.6
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## NA NA NA NA NA
##
## Random effects:
## Groups Name Variance Std.Dev.
## id_int (Intercept) 14.77 3.843
## Residual 31.68 5.628
## Number of obs: 129681, groups: id_int, 14216
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 3.869135 0.056184 68.866
## age 3.534366 0.004078 866.797
## sex 0.336620 0.080317 4.191
## age:sex -0.200629 0.005789 -34.655
##
## Correlation of Fixed Effects:
## (Intr) age sex
## age -0.445
## sex -0.700 0.311
## age:sex 0.313 -0.704 -0.443
##
## $study2
## Linear mixed model fit by REML ['lmerMod']
## Formula: weight ~ 1 + age + sex + age * sex + (1 | id_int)
## Data: dataDF
## Weights: weights.to.use
## Offset: offset.to.use
## Control: control.obj
##
## REML criterion at convergence: 54369.4
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## NA NA NA NA NA
##
## Random effects:
## Groups Name Variance Std.Dev.
## id_int (Intercept) 1.250 1.118
## Residual 3.692 1.921
## Number of obs: 12724, groups: id_int, 951
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 6.03409 0.06151 98.097
## age 2.85790 0.01411 202.581
## sex -0.54661 0.09028 -6.055
## age:sex 0.03661 0.02049 1.787
##
## Correlation of Fixed Effects:
## (Intr) age sex
## age -0.455
## sex -0.681 0.310
## age:sex 0.313 -0.688 -0.456
##
## $study3
## Linear mixed model fit by REML ['lmerMod']
## Formula: weight ~ 1 + age + sex + age * sex + (1 | id_int)
## Data: dataDF
## Weights: weights.to.use
## Offset: offset.to.use
## Control: control.obj
##
## REML criterion at convergence: 292805.1
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## NA NA NA NA NA
##
## Random effects:
## Groups Name Variance Std.Dev.
## id_int (Intercept) 0.6142 0.7837
## Residual 3.6480 1.9100
## Number of obs: 68864, groups: id_int, 13445
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 5.089372 0.016491 308.613
## age 3.119718 0.005986 521.136
## sex -0.394888 0.023685 -16.672
## age:sex 0.004995 0.008556 0.584
##
## Correlation of Fixed Effects:
## (Intr) age sex
## age -0.528
## sex -0.696 0.368
## age:sex 0.369 -0.700 -0.529
##
## $study4
## Linear mixed model fit by REML ['lmerMod']
## Formula: weight ~ 1 + age + sex + age * sex + (1 | id_int)
## Data: dataDF
## Weights: weights.to.use
## Offset: offset.to.use
## Control: control.obj
##
## REML criterion at convergence: 1138299
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## NA NA NA NA NA
##
## Random effects:
## Groups Name Variance Std.Dev.
## id_int (Intercept) 3.402 1.844
## Residual 20.521 4.530
## Number of obs: 191224, groups: id_int, 17046
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 4.689392 0.026376 177.793
## age 3.455656 0.003041 1136.282
## sex 0.013923 0.038018 0.366
## age:sex -0.240527 0.004382 -54.889
##
## Correlation of Fixed Effects:
## (Intr) age sex
## age -0.381
## sex -0.694 0.264
## age:sex 0.264 -0.694 -0.381
##
## $input.beta.matrix.for.SLMA
## betas study 1 betas study 2 betas study 3 betas study 4
## (Intercept) 3.8691347 6.03408780 5.089372058 4.68939189
## age 3.5343657 2.85790465 3.119717700 3.45565555
## sex 0.3366204 -0.54660715 -0.394887544 0.01392347
## age:sex -0.2006292 0.03661021 0.004995405 -0.24052747
##
## $input.se.matrix.for.SLMA
## ses study 1 ses study 2 ses study 3 ses study 4
## (Intercept) 0.056183657 0.06151162 0.016491091 0.026375527
## age 0.004077501 0.01410748 0.005986375 0.003041196
## sex 0.080317421 0.09027731 0.023685373 0.038017878
## age:sex 0.005789246 0.02049084 0.008556005 0.004382080Exploring the output
We can see the coefficients for the fixed and random parts of our model directly from the model object.
Fixed effects coefficients for each cohort are here:
model1.fit$betamatrix.valid## betas study 1 betas study 2 betas study 3 betas study 4
## (Intercept) 3.8691347 6.03408780 5.089372058 4.68939189
## age 3.5343657 2.85790465 3.119717700 3.45565555
## sex 0.3366204 -0.54660715 -0.394887544 0.01392347
## age:sex -0.2006292 0.03661021 0.004995405 -0.24052747The pooled estimates are here:
model1.fit$SLMA.pooled.ests.matrix## pooled.ML se.ML pooled.REML se.REML pooled.FE se.FE
## (Intercept) 4.9201754 0.38859060 4.9202557 0.44896972 4.9643913 0.013250416
## age 3.2421628 0.13538495 3.2420998 0.15635197 3.4176657 0.002229407
## sex -0.1477761 0.17066919 -0.1477464 0.19787562 -0.2576757 0.019061879
## age:sex -0.1008701 0.06092812 -0.1006258 0.07037899 -0.1873971 0.003195114And the details of the random effects are here:
model1.fit$output.summary$study1$varcor## Groups Name Std.Dev.
## id_int (Intercept) 3.8426
## Residual 5.6282A neater way
I find these objects a little fiddly to work with (you may not). You can also use the dsHelper function to extract the coefficients.
model1.coef <- dh.lmTab(
model = model1.fit,
type = "lmer_slma",
coh_names = names(conns),
ci_format = "separate",
direction = "wide")Let’s explore there in more detail
Fixed effects
The fixed effects are analogous to your coefficients from a linear regression model.
model1.coef$fixed## # A tibble: 20 × 9
## cohort variable est se pvalue n_obs n_coh lowci uppci
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 alspac intercept 3.87 0.06 NA 129681 1 3.76 3.98
## 2 alspac age 3.53 0 NA 129681 1 3.53 3.54
## 3 alspac sex 0.34 0.08 NA 129681 1 0.18 0.49
## 4 alspac age:sex -0.2 0.01 NA 129681 1 -0.21 -0.19
## 5 bcg intercept 6.03 0.06 NA 12724 1 5.91 6.15
## 6 bcg age 2.86 0.01 NA 12724 1 2.83 2.89
## 7 bcg sex -0.55 0.09 NA 12724 1 -0.72 -0.37
## 8 bcg age:sex 0.04 0.02 NA 12724 1 0 0.08
## 9 bib intercept 5.09 0.02 NA 68864 1 5.06 5.12
## 10 bib age 3.12 0.01 NA 68864 1 3.11 3.13
## 11 bib sex -0.39 0.02 NA 68864 1 -0.44 -0.35
## 12 bib age:sex 0 0.01 NA 68864 1 -0.01 0.02
## 13 probit intercept 4.69 0.03 NA 191224 1 4.64 4.74
## 14 probit age 3.46 0 NA 191224 1 3.45 3.46
## 15 probit sex 0.01 0.04 NA 191224 1 -0.06 0.09
## 16 probit age:sex -0.24 0 NA 191224 1 -0.25 -0.23
## 17 combined intercept 4.92 0.39 NA 402493 4 4.16 5.68
## 18 combined age 3.24 0.14 NA 402493 4 2.98 3.51
## 19 combined sex -0.15 0.17 NA 402493 4 -0.48 0.19
## 20 combined age:sex -0.1 0.06 NA 402493 4 -0.22 0.02If we use dh.lmTab it allows us to manipulate our output more easily. For example you might want to split the fixed effects by cohort:
model1.coef$fixed %>% group_by(cohort) %>%
group_split()## <list_of<
## tbl_df<
## cohort : character
## variable: character
## est : double
## se : double
## pvalue : double
## n_obs : double
## n_coh : double
## lowci : double
## uppci : double
## >
## >[5]>
## [[1]]
## # A tibble: 4 × 9
## cohort variable est se pvalue n_obs n_coh lowci uppci
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 alspac intercept 3.87 0.06 NA 129681 1 3.76 3.98
## 2 alspac age 3.53 0 NA 129681 1 3.53 3.54
## 3 alspac sex 0.34 0.08 NA 129681 1 0.18 0.49
## 4 alspac age:sex -0.2 0.01 NA 129681 1 -0.21 -0.19
##
## [[2]]
## # A tibble: 4 × 9
## cohort variable est se pvalue n_obs n_coh lowci uppci
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 bcg intercept 6.03 0.06 NA 12724 1 5.91 6.15
## 2 bcg age 2.86 0.01 NA 12724 1 2.83 2.89
## 3 bcg sex -0.55 0.09 NA 12724 1 -0.72 -0.37
## 4 bcg age:sex 0.04 0.02 NA 12724 1 0 0.08
##
## [[3]]
## # A tibble: 4 × 9
## cohort variable est se pvalue n_obs n_coh lowci uppci
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 bib intercept 5.09 0.02 NA 68864 1 5.06 5.12
## 2 bib age 3.12 0.01 NA 68864 1 3.11 3.13
## 3 bib sex -0.39 0.02 NA 68864 1 -0.44 -0.35
## 4 bib age:sex 0 0.01 NA 68864 1 -0.01 0.02
##
## [[4]]
## # A tibble: 4 × 9
## cohort variable est se pvalue n_obs n_coh lowci uppci
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 combined intercept 4.92 0.39 NA 402493 4 4.16 5.68
## 2 combined age 3.24 0.14 NA 402493 4 2.98 3.51
## 3 combined sex -0.15 0.17 NA 402493 4 -0.48 0.19
## 4 combined age:sex -0.1 0.06 NA 402493 4 -0.22 0.02
##
## [[5]]
## # A tibble: 4 × 9
## cohort variable est se pvalue n_obs n_coh lowci uppci
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 probit intercept 4.69 0.03 NA 191224 1 4.64 4.74
## 2 probit age 3.46 0 NA 191224 1 3.45 3.46
## 3 probit sex 0.01 0.04 NA 191224 1 -0.06 0.09
## 4 probit age:sex -0.24 0 NA 191224 1 -0.25 -0.23Or you might want to just select the pooled results:
## # A tibble: 4 × 9
## cohort variable est se pvalue n_obs n_coh lowci uppci
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 combined intercept 4.92 0.39 NA 402493 4 4.16 5.68
## 2 combined age 3.24 0.14 NA 402493 4 2.98 3.51
## 3 combined sex -0.15 0.17 NA 402493 4 -0.48 0.19
## 4 combined age:sex -0.1 0.06 NA 402493 4 -0.22 0.02Random effects
When the model if fit, group (level 2) residuals are calculated for each subject. These represent the difference between interecept of each subject and the mean intercept for the sample.
However, there are not returned by DataSHIELD as they could be disclosive. Instead we can view the standard deviation of these residuals:
model1.coef$random## # A tibble: 8 × 5
## cohort group var1 var2 stddev
## <chr> <chr> <chr> <chr> <dbl>
## 1 alspac id_int intercept <NA> 3.84
## 2 alspac Residual <NA> <NA> 5.63
## 3 bcg id_int intercept <NA> 1.12
## 4 bcg Residual <NA> <NA> 1.92
## 5 bib id_int intercept <NA> 0.78
## 6 bib Residual <NA> <NA> 1.91
## 7 probit id_int intercept <NA> 1.84
## 8 probit Residual <NA> <NA> 4.53If we take ALSPAC as an example, we have an overall (mean) intercept of 3.87, and a standard deviation of 3.84. This indicates considerable variability between individual intercepts. If you had specified more than one random effect (e.g. slope) this would also be displayed here. We can also see the standard deviation of the residual error, ie the difference between observed values and predicted values within subject.
Plotting the trajectories
In order to plot trajectories, we first need to get model predicted values of weight. In order to do this, we need to create a dataframe with the values of the fixed effects at which we want to predict values of weight. The names of the columns of this new dataframe need to correspond to the names of the coefficients in the output above.
We want to visualise the trajectories for both males and females between ages 0 and 25. In our reference dataframe, we therefore create values for age between 0 and 25 at 0.1 intervals, repeated for sex == 0 (males) and sex == 1 (females).
new_data_m <- tibble(
age = seq(0, 25, by = 0.1),
"age:sex" = age*0,
sex = 0)
new_data_f <- tibble(
age = seq(0, 25, by = 0.11),
"age:sex" = age*1,
sex = 1)
pred_data <- bind_rows(new_data_m, new_data_f)If we look at this object we have created, it has all the values of the model variables at which we want to predict weight:
pred_data## # A tibble: 479 × 3
## age `age:sex` sex
## <dbl> <dbl> <dbl>
## 1 0 0 0
## 2 0.1 0 0
## 3 0.2 0 0
## 4 0.3 0 0
## 5 0.4 0 0
## 6 0.5 0 0
## 7 0.6 0 0
## 8 0.7 0 0
## 9 0.8 0 0
## 10 0.9 0 0
## # ℹ 469 more rowsWe can then use this reference data and our model object to get predicted values. Note that we now have four more columns appended to our reference data containing predicted values, standard error of predictions and confidence intervals.
plotdata <- dh.predictLmer(
model = model1.fit,
new_data = pred_data,
coh_names = names(conns))
plotdata## # A tibble: 2,395 × 9
## cohort intercept age `age:sex` sex predicted se low_ci upper_ci
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 alspac 1 0 0 0 3.87 0.0562 3.76 3.98
## 2 alspac 1 0.1 0 0 4.22 0.0560 4.11 4.33
## 3 alspac 1 0.2 0 0 4.58 0.0558 4.47 4.69
## 4 alspac 1 0.3 0 0 4.93 0.0557 4.82 5.04
## 5 alspac 1 0.4 0 0 5.28 0.0555 5.17 5.39
## 6 alspac 1 0.5 0 0 5.64 0.0553 5.53 5.74
## 7 alspac 1 0.6 0 0 5.99 0.0551 5.88 6.10
## 8 alspac 1 0.7 0 0 6.34 0.0550 6.23 6.45
## 9 alspac 1 0.8 0 0 6.69 0.0548 6.59 6.80
## 10 alspac 1 0.9 0 0 7.05 0.0547 6.94 7.15
## # ℹ 2,385 more rowsNice, we’re getting there. One thing to address is that currently we have predicted values for all cohorts between ages 0 and 25. However many of the cohorts don’t have data between those ages, so we might not want to plot beyond where there is data. We can trim our predicted data to the available ages.
plot_trim <- dh.trimPredData(
pred = plotdata,
coh_names = c("alspac", "bcg", "bib", "probit", "combined"),
min = rep(0, 5),
max = c(20, 5, 5, 20, 20))
plot_trim## # A tibble: 1,343 × 9
## cohort intercept age `age:sex` sex predicted se low_ci upper_ci
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 alspac 1 0 0 0 3.87 0.0562 3.76 3.98
## 2 alspac 1 0.1 0 0 4.22 0.0560 4.11 4.33
## 3 alspac 1 0.2 0 0 4.58 0.0558 4.47 4.69
## 4 alspac 1 0.3 0 0 4.93 0.0557 4.82 5.04
## 5 alspac 1 0.4 0 0 5.28 0.0555 5.17 5.39
## 6 alspac 1 0.5 0 0 5.64 0.0553 5.53 5.74
## 7 alspac 1 0.6 0 0 5.99 0.0551 5.88 6.10
## 8 alspac 1 0.7 0 0 6.34 0.0550 6.23 6.45
## 9 alspac 1 0.8 0 0 6.69 0.0548 6.59 6.80
## 10 alspac 1 0.9 0 0 7.05 0.0547 6.94 7.15
## # ℹ 1,333 more rowsNext we set sex as a factor to make the plot clearer:
plot_trim <- plot_trim %>%
mutate(sex = factor(sex, levels = c(0, 1), labels = c("Male", "Female")))It would also be nice to be able to overlay the predicted trajectory with the observed values. Remember earlier we made a scatter plot using DataSHIELD? We can extract the anonymised values which were used in that plot and store them as a local object. This allows us to build more flexible plots.
Each row of the created object represents the anomyised values of a subject.
observed <- dh.getAnonPlotData(
df = "data",
var_1 = "age",
var_2 = "weight")
observed## # A tibble: 804,986 × 3
## cohort age weight
## <chr> <dbl> <dbl>
## 1 alspac 0.130 4.93
## 2 alspac 0.604 7.37
## 3 alspac 3.89 18.5
## 4 alspac 7.64 26.5
## 5 alspac 8.57 30.4
## 6 alspac 10.8 39.4
## 7 alspac 13.0 56.8
## 8 alspac 17.8 84.4
## 9 alspac 1.00 9.79
## 10 alspac 1.36 10.1
## # ℹ 804,976 more rowsNow we are ready to plot the pooled trajectories. We use the function “sample_frac” to only take 1% of the observed values. You can play around with this value, but if you use too many the graph becomes unreadable.
ggplot() +
geom_point(
data = sample_frac(observed, .01) %>% dplyr::filter(cohort == "combined"),
aes(x = age, y = weight),
alpha = 0.4,
size = 0.1) +
geom_line(
data = plot_trim %>% dplyr::filter(cohort == "combined"),
aes(x = age, y = predicted, colour = sex), size = 0.8) +
geom_ribbon(
data = plot_trim %>% dplyr::filter(cohort == "combined" & sex == "Male"),
aes(x = age, ymin = low_ci, ymax = upper_ci), alpha = 0.1) +
geom_ribbon(
data = plot_trim %>% dplyr::filter(cohort == "combined" & sex == "Female"),
aes(x = age, ymin = low_ci, ymax = upper_ci), alpha = 0.1) +
scale_x_continuous(limit = c(0, 20), breaks = seq(0, 20, 5), expand = c(0, 0)) +
scale_y_continuous(limit = c(0, 80), breaks = seq(0, 80, 20), expand = c(0, 0)) +
xlab("Child age") +
ylab("Predicted weight (KG)") +
labs(colour = "Sex")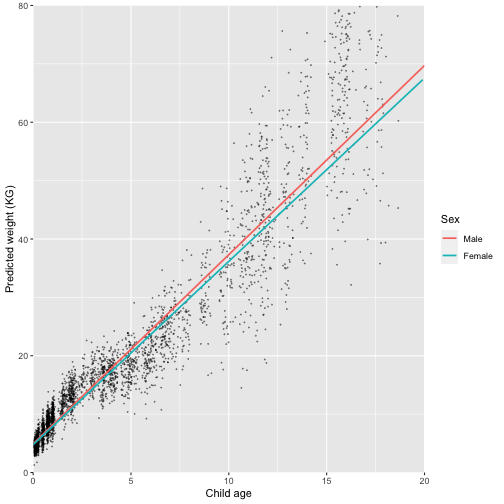
We can also plot the trajectories for each cohort separately:
ggplot() +
geom_point(
data = sample_frac(observed, .01) %>% dplyr::filter(cohort != "combined"),
aes(x = age, y = weight),
alpha = 0.4,
size = 0.1) +
geom_line(
data = plot_trim %>% dplyr::filter(cohort != "combined"),
aes(x = age, y = predicted, colour = sex), size = 0.8) +
geom_ribbon(
data = plot_trim %>% dplyr::filter(cohort != "combined" & sex == "Male"),
aes(x = age, ymin = low_ci, ymax = upper_ci), alpha = 0.1) +
geom_ribbon(
data = plot_trim %>% dplyr::filter(cohort != "combined" & sex == "Female"),
aes(x = age, ymin = low_ci, ymax = upper_ci), alpha = 0.1) +
facet_wrap(~cohort) +
scale_x_continuous(limit = c(0, 20), breaks = seq(0, 20, 5), expand = c(0, 0)) +
scale_y_continuous(limit = c(0, 80), breaks = seq(0, 80, 20), expand = c(0, 0)) +
xlab("Child age") +
ylab("Predicted weight (KG)") +
labs(colour = "Sex")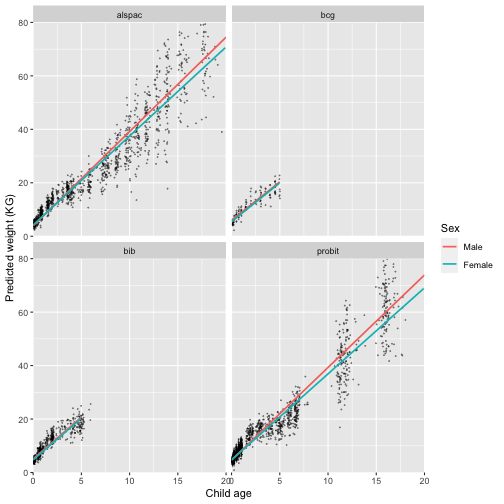
Q: Looking at the plots, how well do you think our model fits the data?
Part 3: Fitting a non-linear trajectory using a transformation of the age term
The previous model doesn’t look great to me, especially around age 5 where there looks to be a distinct non-linearity in the trajectory which we are not capturing.
One way to address this is to model weight not as a function of age, but as a function of a transformation of age.
Let’s start by creating a new variable which is age^2, and see if this provides a better fit. We create the variable, and join it back in our main data frame.
ds.make(
toAssign = "data$age^2",
newobj = "age_2")
ds.dataFrame(
x = c("data", "age_2"),
newobj = "data")Now we are going to simply repeat the steps before, but using this transformed variable instead of the original age variable.
First we run the model:
age_2.fit <- ds.lmerSLMA(
dataName = "data",
formula = "weight ~ 1 + age_2 + sex + age_2*sex + (1|id_int)",
datasources = conns)Now we create a dataframe of the values of the fixed effects at which we want to predict weight. Note that as we have transformed our age term, we need to add this transformed version of the variable to our reference data.
pred_ref_2a <- tibble(
age = seq(0, 25, by = 0.1),
age_2 = age^2,
"age_2:sex" = age_2*0,
sex = 0)
pred_ref_2b <- tibble(
age = seq(0, 25, by = 0.11),
age_2 = age^2,
"age_2:sex" = age_2*1,
sex = 1)
pred_ref_2 <- bind_rows(pred_ref_2a, pred_ref_2b)Again we get the predicted values, trim them at the ages of the observed data and set sex as a factor.
pred_data_2 <- dh.predictLmer(
model = age_2.fit,
new_data = pred_ref_2,
coh_names = names(conns))
pred_data_2_trim <- dh.trimPredData(
pred = pred_data_2,
coh_names = c("alspac", "bcg", "bib", "probit", "combined"),
min = rep(0, 5),
max = c(20, 5, 5, 20, 20))
pred_data_2_trim <- pred_data_2_trim %>%
mutate(sex = factor(sex, levels = c(0, 1), labels = c("Male", "Female")))Let’s plot this against the observed data and see if it fits any better:
ggplot() +
geom_point(
data = sample_frac(observed, .01) %>% dplyr::filter(cohort == "combined"),
aes(x = age, y = weight),
alpha = 0.4,
size = 0.1) +
geom_line(
data = pred_data_2_trim %>% dplyr::filter(cohort == "combined"),
aes(x = age, y = predicted, colour = sex), size = 0.8) +
scale_x_continuous(limit = c(0, 20), breaks = seq(0, 20, 5), expand = c(0, 0)) +
scale_y_continuous(limit = c(0, 80), breaks = seq(0, 80, 20), expand = c(0, 0)) +
xlab("Child age") +
ylab("Predicted weight") +
labs(colour = "Sex")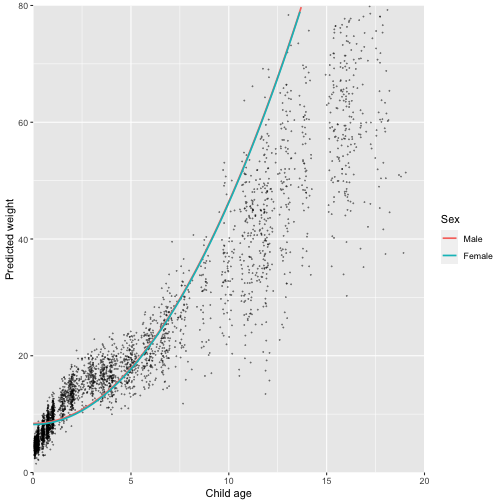
Hmmm. We now have a non-linear trajectory, but it still doesn’t look a great fit. We haven’t looked at any fit statistics or residuals yet, but from the eye it clearly doesn’t fit the data. It also doesn’t seem to capture the sex differences we would expect. We can do better than this.
Part 4: Fractional polynomials
Using one transformation of age allowed one ‘bend’ in the trajectory. However, the problem we saw with the previous model is that natural growth trajectories often have multiple bends.
One way to model this is to use two transformations of age (e.g. age^2 and age^0.5). These are called fractional polynomials (powers which involve fractions). You could use more than 2 transformations: this would give you a better model fit, but with greater risk of overfitting your model. Here we will stick two.
Even with only two transformations of age, there are infinite number of possible combinations. How do we chose which to use?
You may have a good a priori reason to chose a combination of terms. If you don’t, one reasonable approach is to select a certain set of transformations, and fit every combination of those. We can then see which combination of age terms provides the best model fit.
Preparing the data for modelling
Remove values of zero
Transforming values of zero will create infinite values which will break our models. We add a small quantity to our age variable to avoid this.
ds.assign(
toAssign = "data$age+0.01",
newobj = "age",
datasources = conns)
dh.dropCols(
df = "data",
vars = "age",
type = "remove",
new_obj = "data")
ds.dataFrame(
x = c("data", "age"),
newobj = "data")Create transformations of age term
We could do the transformations manually, but this would be a bit cumbersome. We can insted use the function ds.makeAgePolys to create transformations of age. Here we use the following powers: -2, -1, -0.5, log, 0.5, 2, 3.
dh.makeAgePolys(
df = "data",
age_var = "age",
poly_names = c("m_2", "m_1", "m_0_5", "log", "0_5", "2", "3"),
poly_form = c("^-2", "^-1", "^-0.5", "log", "^0.5", "^2", "^3"))We can check this has worked, and see the mean values for these new variables.
poly_summary <- dh.getStats(
df = "data",
vars = c("agem_2", "agem_1", "agem_0_5", "age_log", "age0_5", "age2", "age3")) ## # A tibble: 35 × 4
## cohort variable mean std.dev
## <chr> <chr> <dbl> <dbl>
## 1 alspac age_log 2.13 1.3
## 2 bcg age_log 1.25 0.67
## 3 bib age_log 0.98 0.73
## 4 probit age_log 1.4 1.19
## 5 alspac age0_5 69.2 86.8
## 6 bcg age0_5 6.86 8.19
## 7 bib age0_5 5.25 8.85
## 8 probit age0_5 34.4 72.0
## 9 alspac age2 889. 1393.
## 10 bcg age2 27.0 39.2
## 11 bib age2 22.6 46.0
## 12 probit age2 447. 1125.
## 13 alspac age3 0.78 2.12
## 14 bcg age3 -0.04 1.69
## 15 bib age3 -0.92 2.15
## 16 probit age3 -0.21 2.07
## 17 alspac agem_0_5 1.48 2.59
## 18 bcg agem_0_5 1.68 2.45
## 19 bib agem_0_5 2.95 3.54
## 20 probit agem_0_5 2 2.65
## 21 alspac agem_1 8.89 26.7
## 22 bcg agem_1 8.84 26.0
## 23 bib agem_1 21.2 38.6
## 24 probit agem_1 11.0 28.0
## 25 alspac agem_2 792. 2688.
## 26 bcg agem_2 754. 2628.
## 27 bib agem_2 1945. 3942.
## 28 probit agem_2 905. 2845.
## 29 combined age0_5 39.8 1150
## 30 combined age2 504. 2.18
## 31 combined age3 -0.01 1.23
## 32 combined age_log 1.56 73.8
## 33 combined agem_0_5 1.99 2.84
## 34 combined agem_1 12.0 30.0
## 35 combined agem_2 1042. 3037.Identifying the best fitting model
Ok, so now we have a load of transformations of our age in term in the dataframe “data”. Next we want to fit models for each paired combination of these terms. Again, we could do this by writing out ds.lmerSLMA 28 times, but this brings a fair chance that you make an error in the code.
I’ve written a couple more functions to streamline the process.
Create model formulae
‘dh.makeLmerForm’ creates the model formulae based on the age terms you have created. The argument to “agevars” is a vector of variable names corresponding to the age transformations we created above.
First we try to find the best shape of trajectory, so we create model formulae just with the age terms.
weight_form <- dh.makeLmerForm(
outcome = "weight",
id_var = "id_int",
age_vars = c("age", "agem_2", "agem_1", "agem_0_5", "age_log", "age0_5", "age2", "age3"),
random = "intercept")## # A tibble: 10 × 2
## polys formula
## <chr[1d]> <chr>
## 1 age,agem_2 weight~1+ age+agem_2 + (1|id_int)
## 2 age,agem_1 weight~1+ age+agem_1 + (1|id_int)
## 3 age,agem_0_5 weight~1+ age+agem_0_5 + (1|id_int)
## 4 age,age_log weight~1+ age+age_log + (1|id_int)
## 5 age,age0_5 weight~1+ age+age0_5 + (1|id_int)
## 6 age,age2 weight~1+ age+age2 + (1|id_int)
## 7 age,age3 weight~1+ age+age3 + (1|id_int)
## 8 agem_2,agem_1 weight~1+ agem_2+agem_1 + (1|id_int)
## 9 agem_2,agem_0_5 weight~1+ agem_2+agem_0_5 + (1|id_int)
## 10 agem_2,age_log weight~1+ agem_2+age_log + (1|id_int)This has created a table where each row (a total of 28) contains the formula for a mixed effects model with a different combination of the fractional polynomials.
Fit all combinations of polynomials
The function dh.lmeMultPoly takes as an input to the argument “formulae” a vector of formulae. Here we use the formulae created above. You could also create your own vector of formulae and supply it to the same argument.
If you’ve read Rachel Hughes’ paper, you’ll notice that she first fits models on a discovery sample, and then checks the fit on the remaining sample. I’ve skipped this here for simplicity but it is possible to do this in DS.
This will take a few minutes as we are fitting 28 different models.
poly.fit <- dh.lmeMultPoly(
df = "data",
formulae = weight_form$formula,
poly_names = weight_form$polys)## Error in dh.lmeMultPoly(df = "data", formulae = weight_form$formulae, : object 'weight_form' not foundThere are some converegence warnings. We can see details here:
poly.fit$convergence## # A tibble: 28 × 4
## poly completed message all_converged
## <chr[1d]> <chr> <chr> <lgl>
## 1 age,agem_2 TRUE <NA> TRUE
## 2 age,agem_1 TRUE <NA> TRUE
## 3 age,agem_0_5 TRUE <NA> TRUE
## 4 age,age_log TRUE <NA> TRUE
## 5 age,age0_5 TRUE <NA> TRUE
## 6 age,age2 TRUE <NA> TRUE
## 7 age,age3 TRUE <NA> TRUE
## 8 agem_2,agem_1 TRUE <NA> FALSE
## 9 agem_2,agem_0_5 TRUE <NA> FALSE
## 10 agem_2,age_log TRUE <NA> TRUE
## # ℹ 18 more rowsThe output contains a table with the negative log likelihood for each model in each study, the average rank of that model across all studies and the summed negative log likelihood. The model with the lowest summed log-likelhood across studies contains two powers: age^0.5 & age^2.
poly.fit$fit## # A tibble: 28 × 6
## model alspac bcg bib probit sum_log
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 age0_5,age2 -413072. -25053. -136400. -555192. -1129718.
## 2 age,age2 -414380. -24847. -135066. -562074. -1136366.
## 3 age0_5,age3 -418867. -25055. -136595. -557293. -1137810.
## 4 age,age3 -414581. -25326. -138701. -560576. -1139183.
## 5 age,age0_5 -418305. -25019. -135347. -569398. -1148069.
## 6 age,age_log -419968. -25864. -139284. -570858. -1155973.
## 7 age,agem_0_5 -420377. -26508. -142164. -570741. -1159790.
## 8 age,agem_1 -420403. -26741. -143292. -570683. -1161119.
## 9 age,agem_2 -420409. -26825. -143753. -570701. -1161687.
## 10 age_log,age2 -419517. -27708. -151222. -565902. -1164349.
## # ℹ 18 more rowsIn this scenario we are trying to fit the same model to all cohorts. In other scenarioes you might want to fit a different model to different cohorts. You could still use this table as a reference for the best fitting model, for example for alspac:
## # A tibble: 28 × 2
## model alspac
## <chr> <dbl>
## 1 age0_5,age2 -413072.
## 2 age,age2 -414380.
## 3 age,age3 -414581.
## 4 age,age0_5 -418305.
## 5 age0_5,age3 -418867.
## 6 age_log,age2 -419517.
## 7 age,age_log -419968.
## 8 age2,age3 -420299.
## 9 age,agem_0_5 -420377.
## 10 age,agem_1 -420403.
## # ℹ 18 more rowsFinal model
Ok, so we’ve got an idea what the best fitting combination of age terms will be. Now we can fit our final model, including sex and the interaction with the age terms. We aren’t worrying about other covariates in this example, but of course you could include them.
final.fit <- ds.lmerSLMA(
dataName = "data",
formula = "weight ~ 1 + age0_5 + age2 + sex + age0_5*sex + age2*sex + (1|id_int)")Making plots
Now we can go through the same process as above to make our plot. Again, we need to create our age transformations in the new data to get the predicted values for weight at each age.
pred_ref_final_m <- tibble(
age = seq(0, 25, by = 0.1),
age0_5 = age^0.5,
age2 = age^2,
sex = 0,
"age0_5:sex" = age0_5*sex,
"age2:sex" = age2*sex)
pred_ref_final_f <- tibble(
age = seq(0, 25, by = 0.1),
age0_5 = age^0.5,
age2 = age^2,
sex = 1,
"age0_5:sex" = age0_5*sex,
"age2:sex" = age2*sex)
pred_ref_final <- bind_rows(pred_ref_final_m, pred_ref_final_f)Again we get the predicted values, trim them at the ages of the observed data and set sex as a factor.
pred_ref_final <- dh.predictLmer(
model = final.fit,
new_data = pred_ref_final,
coh_names = names(conns)
)
pred_ref_final_trim <- dh.trimPredData(
pred = pred_ref_final,
coh_names = c("alspac", "bcg", "bib", "probit", "combined"),
min = rep(0, 5),
max = c(20, 5, 5, 20, 20)
)
pred_ref_final_trim <- pred_ref_final_trim %>%
mutate(sex = factor(sex, levels = c(0, 1), labels = c("Male", "Female")))And now we can make some plots
ggplot() +
geom_point(
data = sample_frac(observed, .01) %>% dplyr::filter(cohort == "combined"),
aes(x = age, y = weight),
alpha = 0.4,
size = 0.1) +
geom_line(
data = pred_ref_final_trim %>% dplyr::filter(cohort == "combined"),
aes(x = age, y = predicted, colour = sex), size = 0.8) +
geom_ribbon(
data = pred_ref_final_trim %>% dplyr::filter(cohort == "combined" & sex == "Male"),
aes(x = age, ymin = low_ci, ymax = upper_ci), alpha = 0.1) +
geom_ribbon(
data = pred_ref_final_trim %>% dplyr::filter(cohort == "combined" & sex == "Female"),
aes(x = age, ymin = low_ci, ymax = upper_ci), alpha = 0.1) +
scale_x_continuous(limit = c(0, 20), breaks = seq(0, 20, 5), expand = c(0, 0)) +
scale_y_continuous(limit = c(0, 80), breaks = seq(0, 80, 20), expand = c(0, 0)) +
xlab("Child age") +
ylab("Predicted weight (KG)") +
labs(colour = "Sex")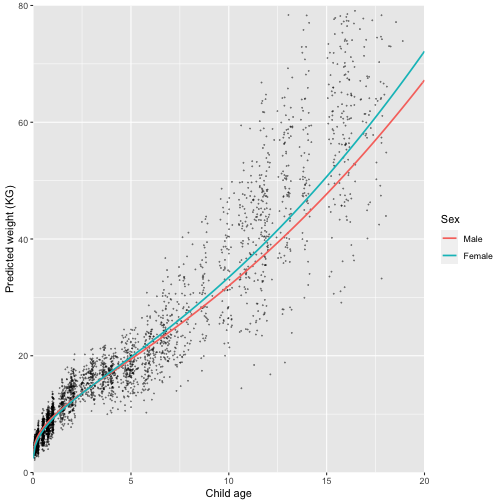
We can also plot the trajectories by cohort
ggplot() +
geom_point(
data = sample_frac(observed, .01) %>% dplyr::filter(cohort != "combined"),
aes(x = age, y = weight),
alpha = 0.4,
size = 0.1) +
geom_line(
data = pred_ref_final_trim %>% dplyr::filter(cohort != "combined"),
aes(x = age, y = predicted, colour = sex), size = 0.8) +
geom_ribbon(
data = pred_ref_final_trim %>% dplyr::filter(cohort != "combined" & sex == "Male"),
aes(x = age, ymin = low_ci, ymax = upper_ci), alpha = 0.1) +
geom_ribbon(
data = pred_ref_final_trim %>% dplyr::filter(cohort != "combined" & sex == "Female"),
aes(x = age, ymin = low_ci, ymax = upper_ci), alpha = 0.1) +
facet_wrap(~cohort) +
scale_x_continuous(limit = c(0, 20), breaks = seq(0, 20, 5), expand = c(0, 0)) +
scale_y_continuous(limit = c(0, 80), breaks = seq(0, 80, 20), expand = c(0, 0)) +
xlab("Child age") +
ylab("Predicted weight (KG)") +
labs(colour = "Sex")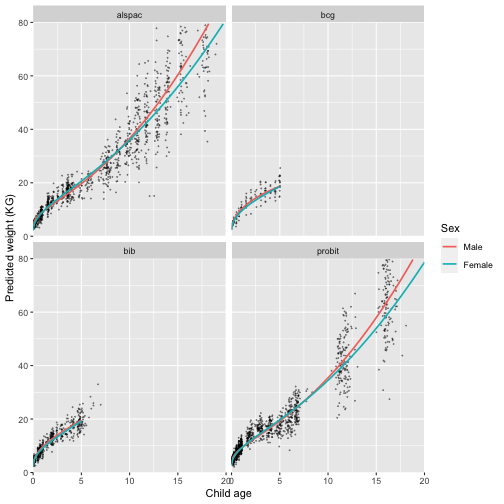
Great, this looks like a much better fit. We have captured the initial growth, followed by a reduction in growth rate at age 5 followed by an increase into adolescence.
This model still isn’t perfect - looking at the graph what problem can you see?
Checking model fit
The final step is to check how well the model fits at different age points. Here we can approximate Table 2 from Tilling et al. (2014) “Modelling Childhood Growth …”.
First we get mean observed values for weight between different age bands. The ‘intervals’ argument specifies how we want to bin our age variable. Again this takes a few minutes to run.
observed_by_age <- dh.meanByGroup(
df = "data",
outcome = "weight",
group_var = "age",
intervals = c(0, 1, 1, 2, 3, 5, 6, 10, 11, 15, 16, 18)
)
observed_by_age## # A tibble: 19 × 6
## cohort group mean std.dev nvalid nmissing
## <chr> <chr> <dbl> <dbl> <dbl> <dbl>
## 1 alspac 0_1 5.79 2.08 37577 92104
## 2 bcg 0_1 6.12 1.92 4949 7775
## 3 bib 0_1 5.39 1.88 40931 27933
## 4 probit 0_1 5.94 1.99 102981 88243
## 5 alspac 11_15 48.6 11.3 20591 109090
## 6 probit 11_15 41.6 9.89 13109 178115
## 7 alspac 16_18 67.3 13.9 4299 125382
## 8 probit 16_18 62.9 12.5 7962 183262
## 9 alspac 1_2 12.0 1.98 10065 119616
## 10 bcg 1_2 11.1 2.19 1882 10842
## 11 bib 1_2 11.8 2.34 7927 60937
## 12 probit 1_2 11.1 2.39 17930 173294
## 13 alspac 3_5 17.0 2.48 14382 115299
## 14 bcg 3_5 16.6 2.66 3582 9142
## 15 bib 3_5 17.6 2.73 11164 57700
## 16 probit 3_5 16.9 2.51 13378 177846
## 17 alspac 6_10 29.1 7.07 20138 109543
## 18 bib 6_10 25.6 4.33 409 68455
## 19 probit 6_10 23.0 4.10 14980 176244We rename our column to ‘observed’:
Now we get the average predicted values between the same age bands
pred_by_age <- pred_ref_final_trim %>%
mutate(
group = case_when(
age > 0 & age <= 1 ~ "0_1",
age >= 1 & age <= 2 ~ "1_2",
age >= 3 & age <= 5 ~ "3_5",
age >= 6 & age <= 10 ~ "6_10",
age >= 11 & age <= 15 ~ "11_15",
age >= 16 & age <= 18 ~ "16_18")
) %>%
dplyr::filter(!is.na(group)) %>%
group_by(group, cohort) %>%
summarise(
predicted = round(mean(predicted), 2),
low_ci = round(mean(low_ci), 2),
upper_ci = round(mean(upper_ci), 2))
pred_by_age## # A tibble: 24 × 5
## # Groups: group [6]
## group cohort predicted low_ci upper_ci
## <chr> <chr> <dbl> <dbl> <dbl>
## 1 0_1 alspac 7.33 7.22 7.44
## 2 0_1 bcg 7.57 7.45 7.69
## 3 0_1 bib 7.38 7.35 7.41
## 4 0_1 combined 7.41 NA NA
## 5 0_1 probit 7.31 7.26 7.36
## 6 11_15 alspac 48.9 48.8 49.0
## 7 11_15 combined 42.2 NA NA
## 8 11_15 probit 47 46.9 47.1
## 9 16_18 alspac 68.7 68.6 68.9
## 10 16_18 combined 56.9 NA NA
## # ℹ 14 more rowsFinally we join the observed and predicted values into one table, and calculate the difference between the two. We can also use the confidence intervals to calculate upper and lower bounds of the residual. You can see that model fit isn’t great for PROBIT towards the extremes. For other cohorts, the looks pretty good.
res_tab <- left_join(obs, pred_by_age, by = c("group", "cohort")) %>%
mutate(
difference = round(observed - predicted, 2),
lower_res = round(observed - upper_ci, 2),
higher_res = round(observed - low_ci, 2),
group = factor(
group,
levels = c("0_1", "1_2", "3_5", "6_10", "11_15", "16_18"),
ordered = TRUE),
limits = paste0(lower_res, " to ", higher_res)) %>%
filter(!is.na(predicted)) %>%
dplyr::select(group, cohort, observed, predicted, difference, limits) %>%
arrange(group) %>%
group_by(cohort) %>%
group_split %>%
set_names(names(conns))
res_tab## <list_of<
## tbl_df<
## group : ordered<59289>
## cohort : character
## observed : double
## predicted : double
## difference: double
## limits : character
## >
## >[4]>
## $alspac
## # A tibble: 6 × 6
## group cohort observed predicted difference limits
## <ord> <chr> <dbl> <dbl> <dbl> <chr>
## 1 0_1 alspac 5.79 7.33 -1.54 -1.65 to -1.43
## 2 1_2 alspac 12.0 10.9 1.11 1.01 to 1.22
## 3 3_5 alspac 17.0 17.4 -0.49 -0.6 to -0.38
## 4 6_10 alspac 29.1 29.4 -0.25 -0.36 to -0.14
## 5 11_15 alspac 48.6 48.9 -0.24 -0.35 to -0.13
## 6 16_18 alspac 67.3 68.7 -1.46 -1.61 to -1.3
##
## $bcg
## # A tibble: 3 × 6
## group cohort observed predicted difference limits
## <ord> <chr> <dbl> <dbl> <dbl> <chr>
## 1 0_1 bcg 6.12 7.57 -1.45 -1.57 to -1.33
## 2 1_2 bcg 11.1 11.4 -0.29 -0.41 to -0.17
## 3 3_5 bcg 16.6 16.9 -0.27 -0.4 to -0.15
##
## $bib
## # A tibble: 3 × 6
## group cohort observed predicted difference limits
## <ord> <chr> <dbl> <dbl> <dbl> <chr>
## 1 0_1 bib 5.39 7.38 -1.99 -2.02 to -1.96
## 2 1_2 bib 11.8 11.1 0.7 0.67 to 0.74
## 3 3_5 bib 17.6 17.2 0.41 0.37 to 0.44
##
## $probit
## # A tibble: 6 × 6
## group cohort observed predicted difference limits
## <ord> <chr> <dbl> <dbl> <dbl> <chr>
## 1 0_1 probit 5.94 7.31 -1.37 -1.42 to -1.32
## 2 1_2 probit 11.1 10.7 0.45 0.4 to 0.5
## 3 3_5 probit 16.9 16.9 -0.02 -0.08 to 0.04
## 4 6_10 probit 23.0 28.3 -5.32 -5.38 to -5.25
## 5 11_15 probit 41.6 47 -5.38 -5.46 to -5.31
## 6 16_18 probit 62.9 66.1 -3.15 -3.26 to -3.04Finish by logging out of the demo server
datashield.logout(conns)